The Avail Programming Language
About Avail
About Us

Guess the Number

Summary

In the game of "guess the number", the proctor arbitrarily selects a number from within a predetermined range and keeps it secret. The player then repeatedly attempts to guess this number. Lest the player should have to rely only on her psychic prowess, the proctor provides hints after each guess about whether the guess was too high or too low. These hints allow a player to direct her search, hopefully using an optimal search strategy like binary search.

In our variant, the part of the proctor will be played by an Avail program, and the part of the player by some poor human who has yet to discover better games.

The previous tutorials focused on trivialities and sweet Avail-centric gimmicks. In this tutorial we are finally going to do some Real Programming™, as you will doubtless infer from the laundry list of goals below.

Playing the game should look something like this:

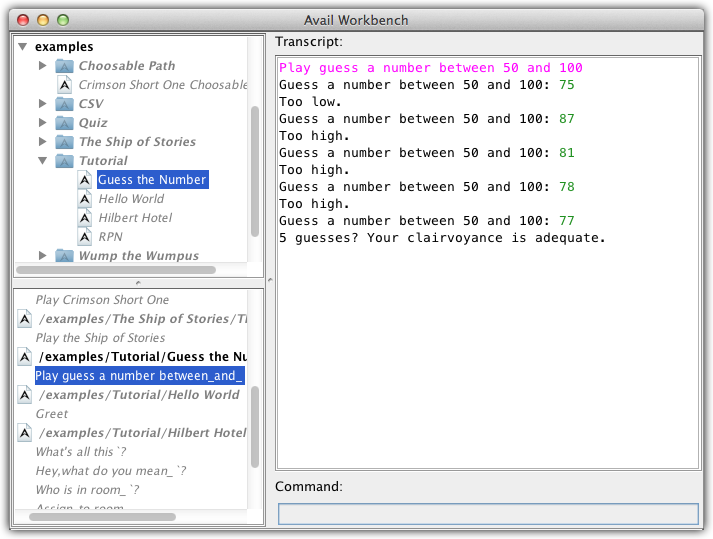
A sample transcript of "Play guess a number between_and_".
The Avail workbench after running "Play guess a number between_and_".

(N.B.: Real Programming is not really a trade mark. At least… it had better not be!)

Prerequisites

  • Understand the material presented in the previous tutorials.

Goals

Complete Sources

Walkthrough

Once again, we are working with just one source module. Go ahead and peruse it now. Stop when your eyes start bleeding. Actually, try to stop before your eyes start bleeding. You're still going to need them for the walkthrough. And you'll probably still want them afterward, even if you don't strictly need them.

Note that this source module has some real heft to it. It isn't just a giant copyright notice with a tiny code snippet dangling helplessly off the bottom. This time there is actually more code than legalese. Let's start by going to line 100.

I can hear you already. "Bucko, aren't we, uh, skipping a whole lot of stuff if we do that?" First of all, my name isn't Bucko, but I'll forgive you the quaint appellation… this time. Otherwise, yes, we are skipping rather a lot of the code. Why? If you glanced through the source module already, like a good reader, then you probably saw some method names that were pretty wild by the standards of traditional programming languages. There is a single primary reason why identifiers are so tame in traditional programming languages: they are very easy to scan from the source text.

But in Avail, methods do not merely have names; they have grammar. The compiler has no idea how to parse an expression unless it has been forewarned about all of the different grammars that combine to form the expression. So before a name can be used, it must either be defined, using something like "Method_is_", or forward declared. Thinking back to the goals for this tutorial, I am already asking a lot from you, so I figured that we should save forward declaration for another time and just define the methods in an order that makes the compiler happy.

In short, we are starting all the way down at line 100 because we needed space to define everything that we are going to use before we actually use it. Capiche? Right! Now stop procrastinating and join me on line 100.

Here we are defining the entry point that allows us to play a game of "guess the number". The method is named "Play guess a number between_and_" and accepts two arguments. The arguments are minimum and maximum, the lower and upper bounds of the range, respectively; both are "integer"s.

There is only one new thing happening here: the use of "Private method_is_" to define a method. This method behaves the same as good old "Method_is_", but imposes the restriction that the new method must not be exported from the module. You don't even know how to export methods yet — well, I didn't tell you how, anyway — so this restriction shouldn't faze you much yet.

"Guess the number" is hardly riveting entertainment, but its dullness would be excruciating without some randomness. Line 105 introduces a local constant named rng and binds it to the return value of the method "a pRNG", which is a pseudo-random number generator (pRNG). A local constant is one that is defined inside a function definition. Its type is the type inferred for the binding expression, i.e., the stuff between ::= and ;, by the compiler, not the type of the value at runtime (because this value isn't available until runtime). Once bound, a local constant cannot be rebound; that's why it's called a constant. (Duh.)

We're not doing anything with our pRNG yet; it just has a name. Line 106 introduces another local constant, theRange, and binds it to the result of sending "[_.._]" to minimum and maximum. The method "[_.._]" constructs an integral type whose arguments establish its inclusive bounds. This notation is chosen to resemble the mathematical notation for intervals, but replaces the (ambiguous and overused) comma with a pair of full stops. This operation might seem a little strange, since you are probably used to dealing with types only at compile time, but in Avail types are first-class values that have great utility.

In Line 107, the electronic proctor finally decides on his target number. The method "_'s⁇next«value in»⁇_" takes a pRNG and a finite integral type and answers, pseudo-randomly, a value that is an instance of the integral type, i.e., a value in the specified range. Without delving too deeply into the funny characters in the method name, it suffices to say that the «…» construct serves to group parts of the method name and ⁇ makes the previous part optional for the programmer to type at a call site. Without any difference in meaning we could have written this call site instead as

theNumber ::= rng' next theRange;

but it would have been much less intelligible. Why have multiple ways to call the method at all then? Because some other call sites might read better with different optional parts plugged in or left out. For example,

someNumber ::= randomNumbers' next [10..20];

leverages the English rules for constructing plural possessives and thus produces a perfectly fine reading. Remember that source code is a literary artifact, and, like all literary artifacts, it is written for humans — not computers. It is very easy to fall into the trap of believing that source code is written for computers, but let's try to leave that pitfall for programmers of traditional programming languages.

Anyway, we can now refer to the target as theNumber. Line 108 uses a helper method defined in this module to determine how many tries it took the player to guess theNumber. Line 109 chooses a suitable (snarky) comment based on the player's guessing prowess, again using a helper method defined nearby. And line 110 prints that comment to standard output. Control falls off the end of the method after this, so the entry point returns and the program exits (but of course leaves the workbench running).

Now that you (hopefully!) understand the program in broad strokes, let's bust out our scalpels and explore the gris(t)ly innards.

On line 59 we see our very first variable. Its name is count, it can store a natural number, and its initial value is 1. It represents the current guess number, so before the player's first guess it is set to 1.

On line 60 we see our (very?) second variable. Its name is guess, its can store an extended integer, and it doesn't have a value yet; it is unassigned. Reading from guess at this point would be very bad, so let's not do it.

So what's the difference between natural number, integer, and extended integer? natural number includes every strictly-positive finite integer; that is, every integer except for zero and the negative integers. Since we are going to use count to track the ordinal of the current guess, and everyone who isn't a programmer starts counting at one, we have chosen a type that better expresses the purpose of the variable. integer subsumes natural number and also includes zero and every finite negative integer. extended integer subsumes integer and also includes ∞ and -∞ as values. As for why we are leveraging the distinction between integer and extended integer here, we will see that shortly.

Lines 61-76 constitute our first control structure. The method "Do_until_alternate with_" implements a loop. Each of its arguments are functions. The first argument is the body of the loop, that is, the central part that is intended to be repeated. The second argument is the predicate, the condition that controls whether to evaluate the body again. The third argument is the interstice, and is only evaluated between two evaluations of the body. This kind of loop works like this:

The body is on line 61. It uses := to assign to guess the result of sending "player's next try for a number in_" to theRange. An assignment is a temporary binding between a variable and a value. This binding lasts until and unless another assignment replaces it later. Only variables can be assigned. We will see what the helper method does in a bit.

The predicate is on line 62. It compares guess to theNumber using the method "_=_". I trust that you guessed that "_=_" compares two values and answers true if and only if they are the same value? Good. The bond of trust between a faceless instructor and an Internet reader is very important.

Lines 64-76 are the interstice, the thing done between two runs of the body. Here we have the logic for responding to an incorrect guess. How do I know that the guess is incorrect? Because the interstice only runs after the predicate answers false; if the predicate had answered true, then the loop would have exited without running the interstice. When the interstice runs, there are three possible situations:

  1. The player provided nonsense instead of a real answer. She may have banged wildly on the keyboard or simply made a typo, who can tell? She might even be trying to crash our program!
  2. The player provided a valid guess, i.e., one within theRange, but it was higher than theNumber.
  3. The player provided a valid guess, but it was lower than theNumber.

Collectively, lines 65-75 handle these three cases. The method "If|if_then_«else if_then_»«else_»" is the all-terrain conditional control structure. Forget about the weird metacharacters in the name and just focus on how we are using this method in the code; we will introduce the concepts associated with these metacharacters in a later tutorial. Suffice to say, you can have one If … then […] fragment, zero or more else if […] then […] fragments, and zero or one else […] fragment. Before we break down this specific usage, let's look up at line 42:

(Ah, how apropos to see 42 and ∞ so close together… but I digress.)

This looks just like the many local constant definitions that we have seen so far, but this one doesn't occur inside a function definition. That makes it a module constant. Module constants are visible to all lexically subsequent expressions, i.e., expressions occurring after the module constant definition in the source module. ∞ is positive infinity. Since we require a finite range for our game, we know that the ∞ is never a valid target number. We give it the name sentinel here to reflect its purpose: in computer science parlance, a sentinel is a value that is never valid for a particular class of usage.

Back to line 65. "player's next try for a number in_" answers sentinel when the player furnishes silly input, and here we check for that case. If guess equals sentinel, then we perform the function after then… which doesn't do anything. This is because it only contains a comment. Comments occur within /* … */ and serve to inform about the programmer's intent. Comments also nest; you can put one comment completely within another. This makes it easy to comment out, i.e., hide from the compiler, large sections of code while you are testing and debugging — even when those sections already contain comments.

Lines 66-70 handle the second case: the player gave a valid response, but it was too high. On line 66 we effect the comparison between guess and theNumber using the method "_>_", which, as you rightly suspect, answers true only when the left argument is greater than the right. There is a very good reason why this predicate is enclosed in square brackets, but, respectfully, I'm not going to tell it to you right now. For the moment, just remember that every predicate in a conditional except for the first must be enclosed in square brackets. (But for the irately curious — those of you who demanded to hear all about double integrals when you first encountered formulae for volume; you know who you are! — make a mental note that I mumbled something about "deferred evaluation of functions" while I was waving my hands about.) Line 69 increments count by 1, since we are about to give the player a chance to guess again. Note that we deliberately didn't adjust count in the first case, because we generously decided not to punish the player for feeding us garbage.

Lines 71-75 handle the third case: the player's response is valid, but too low. We print a hint and update count.

We see a lonely count hanging out on line 77. It doesn't even have a semicolon to keep it company. Now that, ladies and gentlemen, is true loneliness. What's going on here? Semicolons are only permitted after statements. Recall that a statement must produce a side effect, like assigning to a variable or printing to standard output. This is actually the return expression, which gives the enclosing function its value. Think of it as the main effect of the method; the raison d'être of "tries to guess_from range_" is to determine how many guesses it took the player to unmask theNumber. count is pregnant with our method's magnum opus, so we mention it as the last expression of the function to make it available to the caller ("Play guess a number between_and_"). The actual value produced by a return expression is called the return value.

Okay, so… how did we actually interact with the player in the first place? So far all we've seen is the processing of that interaction as a fait accompli. (This ends the multilingual section of this tutorial, promise!) Let's go investigate that helper method, "player's next try for a number in_".

Lines 48-50 are really just a glorified "Print:_", but something cool is happening here. The argument is a formatted "string". The method "format_with«…::=_‡,»" takes a pattern string followed by a comma-separated list of format bindings. A pattern contains zero or more format sites, each of which is a quoted format parameter. When the quotes are left “ (U+201C) and right double quotation mark ” (U+201D), then the value bound to the format parameter is stringified first using "“_”" When the quotes are left ‘ (U+2018) and right single quotation mark ’ (U+2019), then the value bound to the format parameter is expected to already be a string (and will not be stringified). A format binding looks just like a constant definition, to remind you that a format parameter can only assume one value during an interpolation of a pattern, much like a function parameter can only assume one value during an application of a function. The compiler will protest if any of the format parameters are not bound by a format binding, or if a non-string has been supplied as a format value where a string is expected.

In this case, the format parameters are minimum and maximum, and represent the lower and upper bounds of theRange, respectively. The method "⎣_⎦" — pronounced floor — answers the lower bound of an integral type. Conversely, the method "⎡_⎤" — pronounced ceiling — answers the upper bound of an integral type. The net result is really straightforward: we are plugging the bounds of theRange into the corresponding format parameters of the pattern so that we end up with a message like:

Guess a number between 50 and 100: 

Line 51 packs a lot in. Let's pick it apart from the outside moving inward. The method "try_else_" accepts two arguments, both of which are functions. It attempts to evaluate its first argument, called the protected function, producing its return value if it runs successfully to completion. But if anything goes wrong, then it evaluates its second argument and produces its return value instead. The technical elaboration of "anything goes wrong" is "an exception is raised", but that's wading into deeper waters than this tutorial is prepared to plumb.

The protected function does two things. First, it asks "next line«from standard input»⁇" to obtain a line of text from standard input, i.e., the user. This method reads until it discovers a line feed, then answers everything up to, but not including, the line feed as a string. There are many things in theory and practice that can go wrong with reading from standard input, so this operation can definitely "raise an exception", whatever that means. Assuming that it managed to read a line, which is a very good assumption, it then attempts to convert that line into a value in theRange. Clearly this will only work if the user entered a (decimal) numeral like "75" rather than, say, a historical misquote like "I see no ships!". So this too can "raise an exception". Good thing we put these problematic expressions in a protected function!

If the protected function does fail, whether or not it was because of outrage at historical inaccuracy, then "try_else_" answers sentinel to let the caller know that the user flubbed.

(Note that there are much more sophisticated techniques for dealing with exceptions, but we don't require anything grander than "try_else_" for this example.)

You're so good at this now that I'm only going to cover one line of "comment for_tries given a range of_". Line 86 has a whole lot of dense mathematical junk, but only a couple of new things.The method "log_of_" accepts two arguments, a base and a target, and computes a logarithm to find the target's exponent. In this case, we are computing the logarithm base 2 of the larger of 2 and the number of integers within range. Can you guess what this whole line is about? It computes the approximate number of guesses that are required to find the proctor's number using a binary search strategy, fudging in the user's favor. Do you know how I know? It says so in the comment on line 85, and comments never lie… Liars do comment though, but fortunately they aren't doing so here.

Well… I guess that there's one more thing that I ought to cover, since you insist. Notice that if starts with a lowercase letter this time instead of an uppercase one? And that there are no semicolons in sight on lines 87-97? Each […] expression is a separate function definition. So the contents of the square brackets on line 87, lines 90-91, and lines 95-96 are each return expressions; each answers a formatted string. And, in turn, the entire conditional is a return expression. The fancy way that "If|if_then_«else if_then_»«else_»" is named permits the initial keyword to be specified as either If or if. Whenever an Avail programmer is given such a choice, by convention she chooses the keyword beginning with an uppercase letter when using a method as a statement and the lowercase option when using the method as an expression. Here we are using the conditional as an expression that produces one of three different values. Because each function answers a string, the compiler infers that the entire conditional will produce a string. And since the conditional is the method's return expression, this entire method will produce a string. Q.E.D.

That just about wraps things up. We are pseudo-randomly choosing a target number, plying the user in a loop to guess it, giving the user helpful feedback about their guesses, and displaying a modestly pithy message when she finally does guess the right answer. We even handle out-of-range numbers and famous misquotations. What more could a program possibly want out of life?

Well… What happens if the user supplies perverse values to "Play guess a number between_and_"? It says that it requires its arguments to be integers, so we don't expect to be able to build a command with totally inappropriate arguments. Let's see what happens if we try.

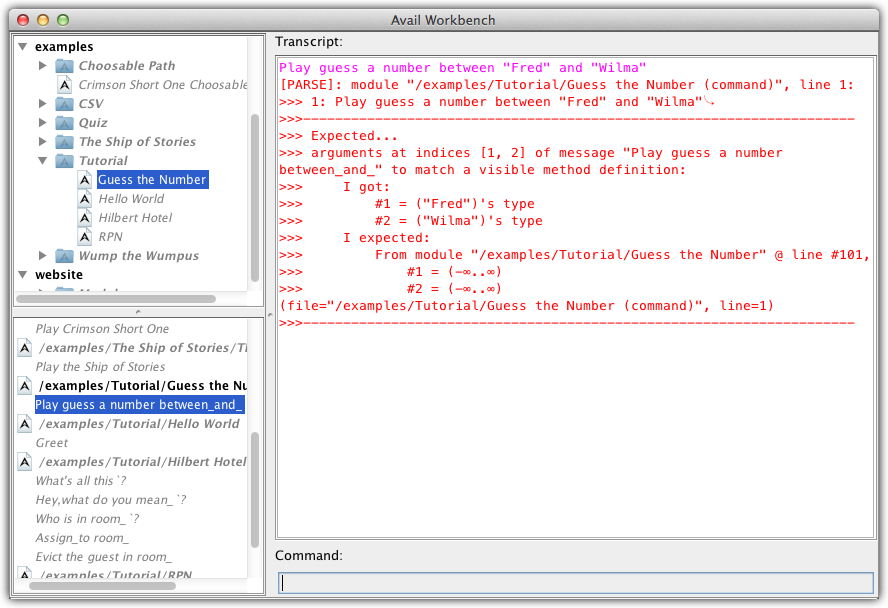
Attempting to "Play guess a number between_and_". with Flintstones.
An erroneous send of "Play guess a number between_and_".

See? The compiler handily defeated our puerile attempt at flippancy. So we'll just have to try harder to break the program. How about we run the command with a minimum that is larger than the maximum? The parameter declarations just say that the arguments have to be integers, not that the first one has to be smaller than the second one. In fact, there isn't any way to define the parameter types to express this idea short of resorting to explicit ranges like [50..100] and [200..300]. But we can see that a command like Play guess a number between 20 and 10 is stupid, so what can we do about it?

There are many approaches to dealing with this issue, but I've chosen to showcase one that is unique to Avail. Let's make the compiler itself reject a command whose minimum and maximum are reversed.

A semantic restriction is a function that is applied by the compiler to the inferred types of the arguments of the named method. It operates not on values but on types. To be precise, a semantic restriction operates on the types inferred by the compiler at the call site of the method. During compilation of a call site, the compiler itself invokes, in parallel, every semantic restriction that is applicable to the inferred types of the supplied arguments. A semantic restriction uses the type information available at a call site to perform two general activities:

  1. Deciding whether to permit or reject a parse.
  2. Deciding what type to infer for the call site.

In this example, we will only consider the first activity.

The parameter declarations of lines 115-116 resemble those of lines 102-103 but they are shifted up one level; they are metatypes rather than types. A metatype is a type whose instances are themselves types. It's more than a little bit wiggy, and just a tad bit whack, but it's very powerful — and it does become easier with time and practice. In fact, we've already seen these metatypes in several of our helper methods already.

Now that we've demystified semantic restrictions a little bit, let's take a good look at the code. It's really pretty simple. There's a conditional (lines 118-122) and a return expression (line 123). The return expression answers ⊤ (U+22A4), pronounced top, the root of the Avail type lattice. When used as the return expression in a semantic restriction, this is an Avail idiom that means "do not strengthen the inferred type of this call site", and we can ignore it. (We will worry about why it means this in a later tutorial.)

So let's concentrate on the conditional. Line 118 asks if the lower bound of minimumType is greater than the upper bound of maximumType. If so, then there is no instance of minimumType that is smaller than any instance of maximumType. When that is the case, then it is guaranteed that the user is trying to supply the arguments in the wrong order. Lines 120-121 use "Reject parse,expected:_" to instruct the compiler to reject the parse of this call site. The compiler records the supplied message to report if and only if it should later decide to terminate the exploration of a top-level statement's meaning because every possible parse was invalid in some way. If the compiler does decide to abandon the parse, then this message will be issued when the compiler's error report is printed. Since this semantic restriction will only run on commands that represent external call sites of "Play guess a number between_and_", our custom parse rejection is pretty much guaranteed to show up. If that was a whole lot of technobabble, then hopefully a screenshot will clear things up:

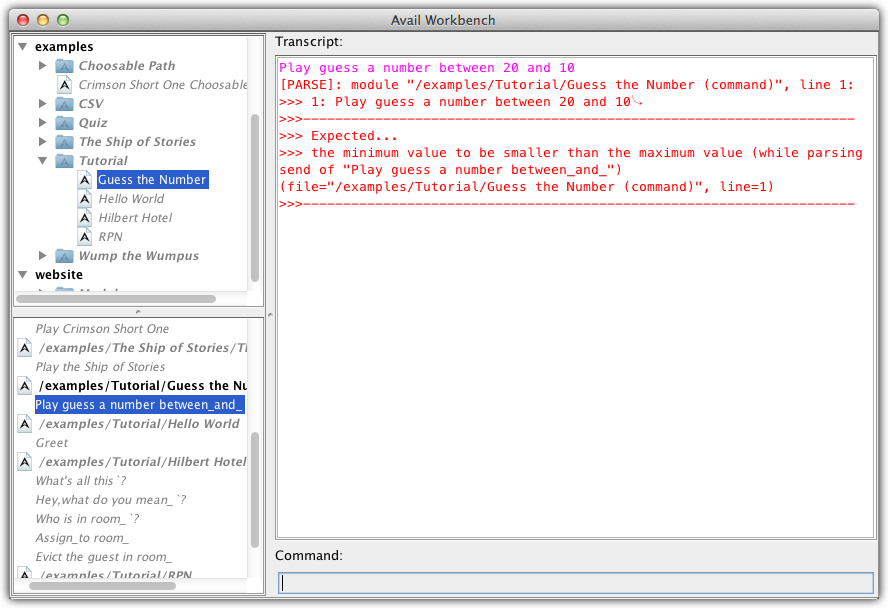
Attempting to "Play guess a number between_and_" with the arguments reversed.
Another erroneous send of "Play guess a number between_and_".

See? A picture really is worth a thousand words. Well, a thousand of my words, anyway…

Further Exploration

If you have the superlatively good fortune to be an etymology nerd, then you might want to learn more about the quaint appellation that you used earlier when you were sassing me.

If you would like the learn the difference between random number generation and pseudo-random number generation, then read up on the topic here.

If you are interested in what Horatio Nelson really said at the Battle of Copenhagen, then go read about it here.

If you want to read about why it is, or is not, a good reason to cite Wikipedia so very much, then read about it here while suppressing a smirk of irony.

If you didn't understand why 42 and ∞ were juxtaposed above, then I highly recommend that you read Douglas Adams' The Hitchhiker's Guide to the Galaxy. It's true comedy gold for the modern age.

Oh, I suppose that you might also want to read more about Avail. In that case, see what the manual has to say about semantic restrictions.

Exercises

  • It's time to put what you've learned about Avail and number guessing games to good use: implement a variation of Mastermind that uses four pegs and six colors. You can represent the different pegs with variables and the different colors with integers. (Or you can get fancier and use tuples instead of variables to represent the different peg positions.)
‹ Reverse Polish Notation | Return to Learn | The Hilbert Hotel ›
© 2012-2023 The Avail Foundation
|
RSS Facebook Twitter Email
|
Our Policies
|
Report an Issue