Reverse Polish Notation

Summary

Reverse Polish Notation (RPN) is an arithmetic notation in which the operators follow their operands. Assuming operators with fixed arities, this postfix operator scheme obviates the need for parentheses. There are also several studies that indicate that users of RPN calculators make fewer mistakes than users of formula calculators.

At some point during formal education, many computer science students are tasked with creating an RPN calculator. There are several different approaches to this project, depending on the pedagogical emphasis, but perhaps the most common involves building a parser that accepts an RPN formula and uses a stack-based interpreter to produce a result.

In this tutorial, we remove all possible educational opportunities from the task of building an RPN calculator by presenting a technique that allows a programmer to bypass all that tedious mucking about with parsers, stacks, and interpreters.

As a bonus, our RPN domain-specific language (DSL) interoperates directly with regular Avail code. Securing the same bonus in a traditional programming language involves rebuilding its parser, thereby causing it to no longer be the original language. Avail, on the other hand, is designed to sail the ship of Theseus all the way home.

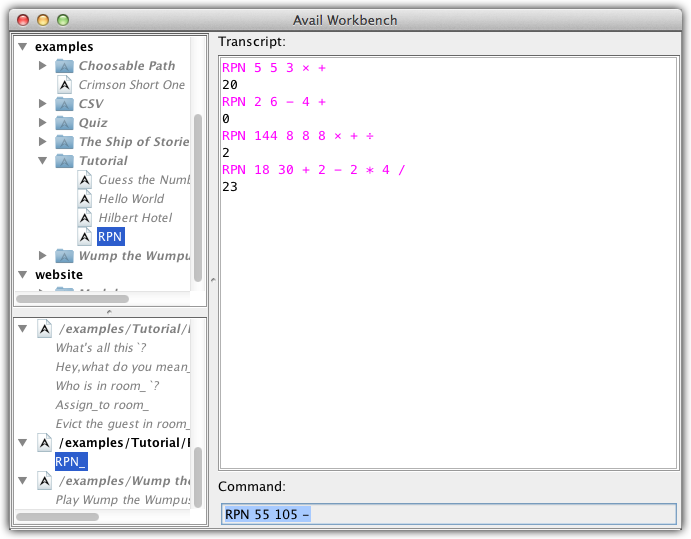
Running the program should look something like this:

Prerequisites

• Understand the material presented in the previous tutorials.

Goals

• Learn how to re-export imported method names for use by other modules.
• Learn how to use a custom import rules list.
• Learn how to rename an imported method name.
• Learn the four basic arithmetic methods, "_+_", "_-_", "_×_", and "_÷_".
• Learn how to "stringify" an arbitrary value using "“_”".

Complete Sources

• RPN.avail

Walkthrough

This project comprises just one small source module. Let's turn our attention to it now.

Lines 34-35 just import the standard library. Big deal. We've already seen this, so let's move on.

Lines 36-45 also imports from the standard library, but there are several new twists here. The Extends keyword enumerates modules that should be imported, just like Uses, but it also re-exports any imported features for use by other modules downstream.

Now notice the equals and the parentheses. This syntax establishes an import filter. An import filter allows you to cherry pick the method names that you want to access. (Obviously, the only names available for cherry picking are those which the target module exports.) In this case, we are importing the methods "_+_", "_-_", "_×_", and "_÷_". But we are not importing them under their given names…

Check out the structural similarities of lines 39-44. Each line comprises a pair of string literals separated by a rightwards arrow → (U+2192). The first string is the name of an exported method. The second string is the name by which that method should be known locally. So the pairing expresses the programmer's desire to rename. Because these renames occur inside the Extends section, these old methods are visible in downstream importers of "RPN", but only by their new names. Indeed, these methods would not even be visible in this module under their original names, except that they were imported implicitly, with their original names, in the Uses section.

Taking line 41 as a concrete example, the standard library, Avail, exports a method "_×_" which we would like to call "__×" in the body of this module. Note that this is two blanks, each of which represents an argument position, followed by a multiplication sign × (U+00D7). As you probably guessed, this method multiplies two "number"s — the multiplicand and the multiplier — together to obtain their product. But in this module and its importers, these operations use postfix notation rather than infix notation. Through the alchemy of method renaming, lines 39-44 conjure our RPN DSL into existence virtually ex nihilo. We didn't need to build a single method in order to write the RPN DSL!

One more thing. Lines 41-42 each have "_×_" on the left, and lines 43-44 each have "_÷_" on the left. This is fine, because each righthand side is distinct. We simply end up with two renames of "_×_" and two renames of "_÷_". The first rename in each pair creates a pretty postfix name, and the second one creates a pragmatic ASCII name that is easy to type.

Lines 50-56 define the method "RPN_". On line 53, expression : number is a parameter declaration which introduces a parameter named expression of type number. The parameters of a function are supplied in the same order as the argument positions specified by the method name. "RPN_" has a single argument position, the blank, which corresponds to the only parameter declaration of the function. The vertical line on line 53 visually separates the parameter declarations from the function body. (It is also a possible nod to Smalltalk's many influences on Avail, but we can forgive it that.)

Line 54. Here we see another call site of "Print:_". But something interesting is happening here. Recall that "Print:_" requires a "string", and expression is a number. See those "smart quotes" — left “ (U+201C) and right double quotation mark ” (U+201D), respectively — around expression? This is a call site of the method "“_”", the stringification method. It accepts an arbitrary value — an instance of any — and produces a string that represents that value textually. In the case of a number, it will produce a suitable numeral. The compiler arranges for the two methods "Print:_" and "“_”" to compose in the only way that is semantically valid, so at runtime "“_”" will run first and "Print:_" will run second (on the stringifier's result).

Since line 47 names "RPN_" as an entry point, Avail uses the grammar exported by "RPN" rather than the grammar available to RPN in deciding how to parse an external call site.

Recall RPN 55 105 - from the Command input field of the workbench presented in the Summary. This RPN formula constitutes an external call site of the method "RPN_", because it is compiled and executed external to any source module. The Command text field of the Avail workbench is always an external call site. The complete text of an external call site is called a command. The top-level syntax available at an external call site is the union of all entry points belonging to loaded modules.

For our purposes, assume that the only top-level syntax available here is "RPN_", and the only subordinate syntaxes that are both grammatically and semantically valid as input at the external call site are:

• "__+",
• "__-",
• "__×",
• "__*",
• "__÷",
• and "__/".

No other expressions are legal here, so our program really is a complete RPN DSL. It has exactly those facilities which we explicitly provided, and no others. As proof of this point, this is what happens if you try to use an infix arithmetic operator in an "RPN_" command:

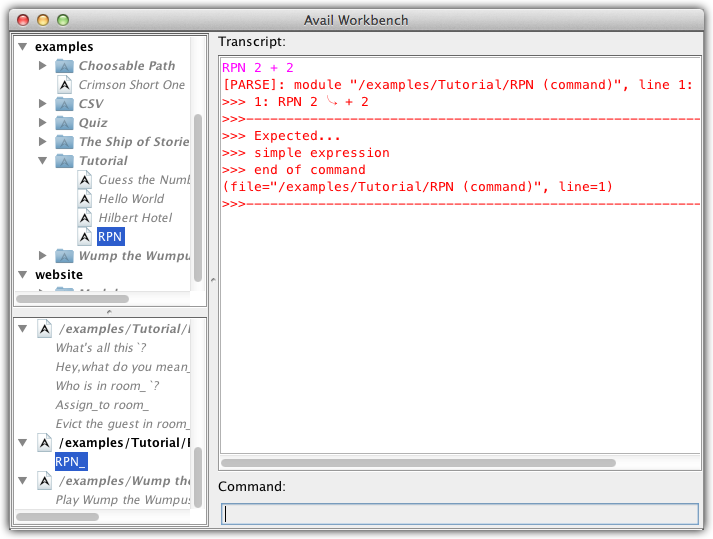
That mess of red text is the compiler's way of informing you that something went wrong. In this case, the Expected... simple expression message means that the compiler was expecting a literal value, like a numeral, rather than an operator like +… because we took away all of the infix operators! (Expected... end of command means that the compiler would have been happy if the whole command had just been RPN 2.)

Further Exploration

For those who wish to learn more about calculator input methods, try starting here.

If you have an interest in Greek mythology, then you may wish to read more about the founder-hero Theseus. His legendary voyage from Crete to Athens inspired philosophers like Plutarch, Thomas Hobbes, and John Locke to wonder about the nature of identity, a topic that is not only intriguing in its own right but also central to the Avail programming language.

Exercises

• Add missing functionality to the RPN DSL. Start with exponentiation ("_^_") and factorial ("_`!"), then go wild. In case you are wondering, the grave accent ` (U+0060), or backtick, is a message metacharacter. It is the escape character, and disables the special meaning of the following metacharacter, in this case exclamation mark ! (U+0021). You do not need to type it in order to send the factorial message.
• Implement arity-2 versions of Scheme's arithmetic operators using the method renaming strategy. To get you started, the addition operator should be named "(+__)". You can safely extrapolate from there.

‹ Hello, world!

|

Return to Learn

|

Guess the number ›